

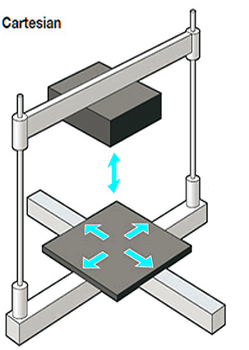
Cartesian 3D printers, the most popular design found in consumer 3D printers market. Cartesian 3D printers are named after the dimensional coordinate system — the X, Y, and Z-axis, which is used to determine where to move a print head in three dimensional space. The print bed in Cartesian 3D printers typically moves only in the Z-axis. The extruder sits on the X-axis and Y-axis, where it can move in four directions on a gantry. |
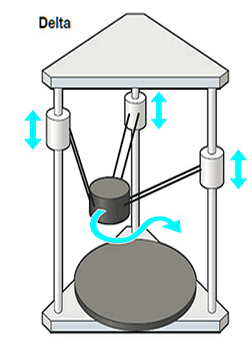
Delta printers use three independent arms on a series of vertically moving rails. These print heads travel horizontally, too. Delta printers use trigonometric functions to coordinate these heads, depositing 3D filaments. The moving parts which make up the printing mechanism are more lightweight and travel in a taller space than a standard Cartesian model. |

The Core-XY is a two-axis linear motion implementation developed at MIT Media Labs. The design itself is open source and it's spreading around the 3d printer community as common design choice. Overall, it delivers the same benefit of the H-bot, a light moving platform, by keeping both motors fixed to the frame rather than mounting one motor on the moving axis. Furthermore, by crossing the belt, the unwanted torque vectors are eliminated. |
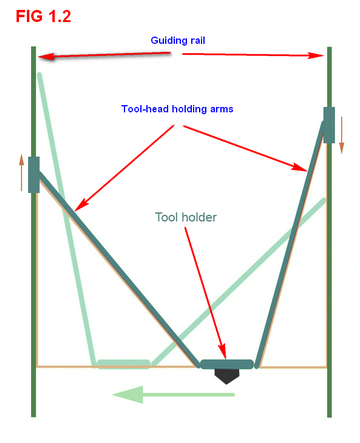
A CoreXZ is also a parallel manipulator system. All the motors in CoreXZ design are stationary. The advantage of parallel manipulator systems, such as CoreXY, H-bot and Dualwire-Gantry (DW-G), typically have much lower inertia than serial stackup arrangements (when using the same motors and the same forces). CoreXZ design uses two independent arms on vertically moving rails/guides. Arms provide positioning of tool holder (extruder) on X and Z axis. The moving print bed (similar to one in Prusa or RepRapPro Mendel) provides positioning on Y axis. |
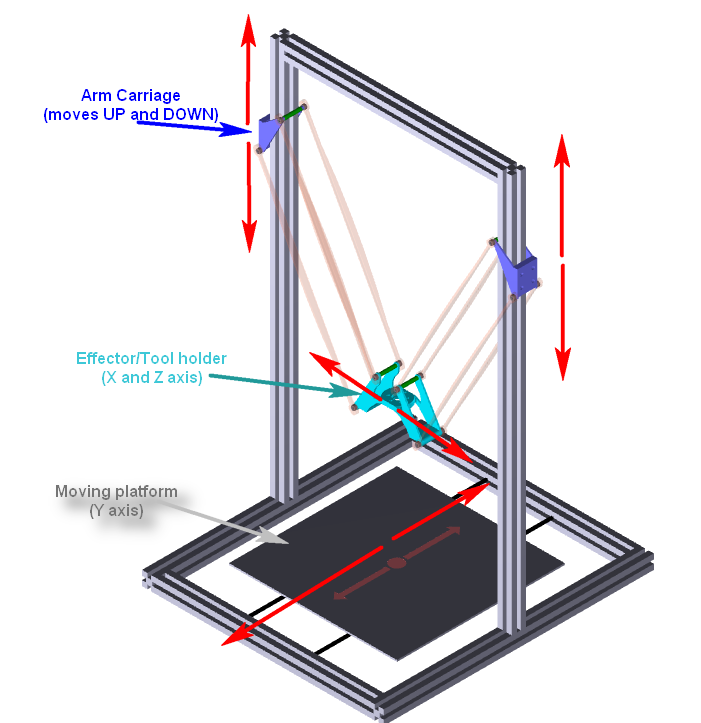
The CoreXZ design allows to use advantages of both worlds - it could be as fast as Deltas (as it uses a light moving platform without sacrificing print space), and accurate as Cartesian 3D printers. Whole kinematics is very simple and does not require trigonometric calculations. It's very easy scalable and could be practical in applications that require fast and precise movements in 3 dimensional space (assembly lines for example).